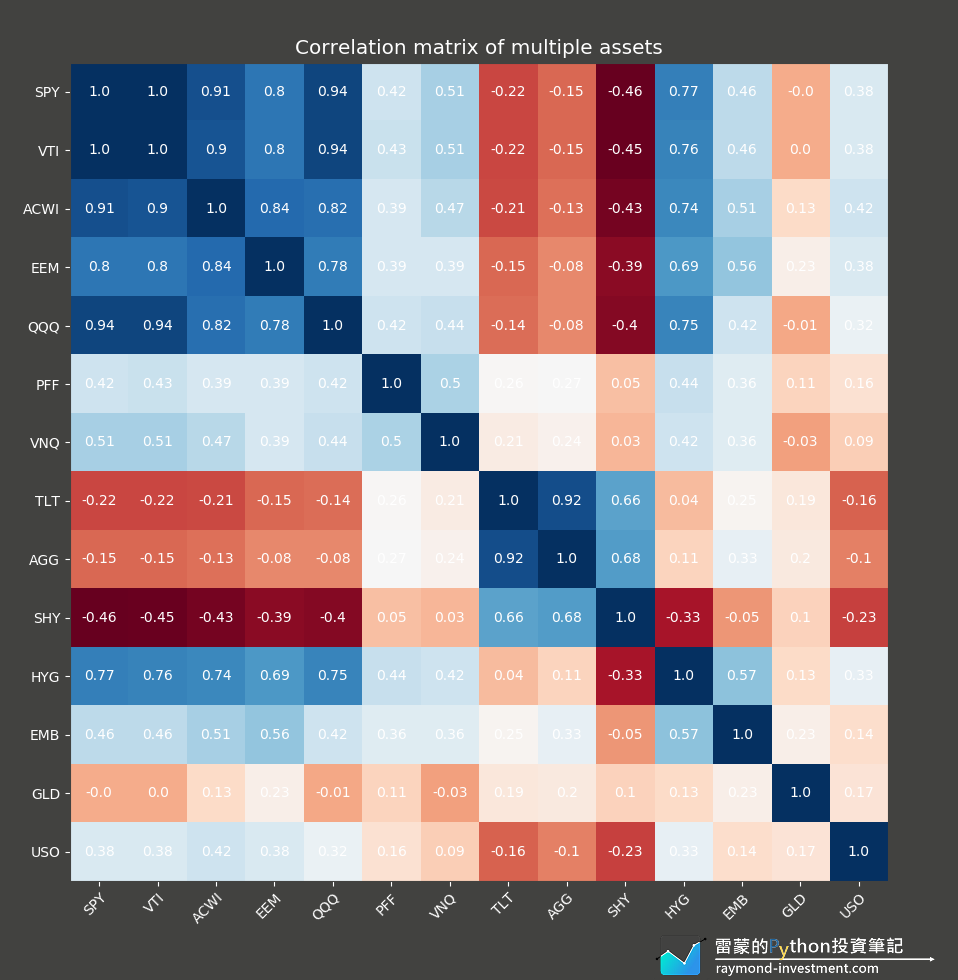
上圖為2018年初至2018年10月的各資產報酬率相關係數矩陣,X軸與Y軸是一樣的,可以查找各資產的相關係數配對,例如我們可以先鎖定第一行SPY的數列,可以找出SPY與EEM的相關係數為0.8,或SPY與SHY的相關係數為-0.46,依此類推,可以找到所有資產彼此間的相關係數。
相關係數是多元資產配置的關鍵參數,透過各資產相關係數越低,將越具有風險分散的效果,相關係數太高不具有太多的分散風險效果,例如同時買進連結S&P500與NASDAQ指數的ETF,類型均為美國股票,且權重重疊之處相當多,兩者相關係數為0.94,可以解釋為「當SPY漲1%時,QQQ平均會上漲0.94%」,並不具任何分散風險的效果。

上圖是實際回測SPY與QQQ組合的狀況,整體走勢幾乎相同,平均報酬率沒有增加非常多外,承擔的波動反而加大了,導致Sharpe值還下降。
如果是持有相關係數為負的資產呢?例如同時持有美股與美國公債,相關係數約為0~-0.5間,在股市大跌時,美債價格容易上漲,以抵銷部分股票下跌的損失,又持有美債有固定的收益,同時持有兩個相關性為負,且具有收益性質的商品是效率資產配置的必要條件。

SPY與TLT就是屬於一個股債平衡的投資組合,透過下表的數據有可以知道資產配置的效果了。
| 投資組合 | 年化報酬率 | 年化波動率 | Sharpe值 |
| SPY | 11.56% | 18.04% | 0.64 |
| TLT | 6.63% | 13.41% | 0.49 |
| SPY 50% + TLT 50% | 9.22% | 9.10% | 1.01 |
是不是持有負相關越高的資產越好呢? 如果持有反向ETF,相關係數可達到-0.9以上,但持有反向ETF是固定付出成本的概念,並不是像公債一樣收到收益,對於資產配置而言並不屬於有效果的部位。
雷大的Python投資筆記電子報
歡迎訂閱雷大的Python投資筆記電子報,每週將會發布定期市場分析文章與不定期的專案研究文章:
- 國際金融市場分析
- 量化交易策略分享
- Python程式撰寫教學
立即訂閱最新文章